2006/09/22
日曜大工において大半の計算は加減乗除の四則計算でまかなえますが、角度の測定あるいはある角度を割り付ける場合には平方根の計算や三角関数を使えば効率よく精度の高い作業になります。 角度の測定や割付と言うと先ず思い起こすのは分度器を使う方法かもしれません。 また大工道具にプロトラクターという角度を測ったり割付したりする物もありますが、価格が1万円以上と高い上にそれを使っても0.5度の目盛りが最小目盛りですから目分量で0.25度辺りを読み取るのが限界です。
JIS規格に適合した曲尺では±0.06度近くの高精度の直角度を有していますからそれに比べると0.25度程度までしか読めないのは精度の点で不十分と言わざるを得ません。 ±0.06度というと大変微量ですから日常では無関係なように思えますが、決してそんなことはありません。 例えば襖を閉めた際に下はぴったりと柱に襖が接触しているにも拘わらず上の部分で2mm隙間が出来てしまうなんていうのは結構現実に存在すると思います。 この場合襖の高さを1,800mmとすると2mmの隙間は0.06度になります。 こう考えると微量ですが誰でも認識できる量でもあるわけです。
よって実用性が極めて高くしかも余計な出費をしないで済む角度の正確な測定方法や割付の仕方を解説しようというのが、このテーマの趣旨です。 平方根の計算や三角関数を使うことに慣れている方にとってはつまらないテーマでしょうが、日常生活で殆ど使うことはないと思うのですっかり忘れてしまった！！という方は、思い出して頂くきっかけになればと思います。
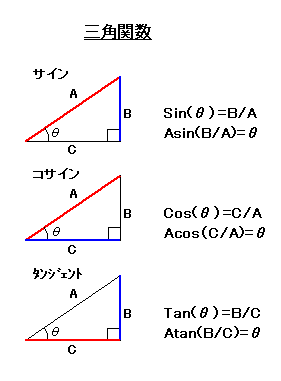三角関数には正弦（サインと読み式ではSinと表現）、余弦（コサインと読
み式ではCosと表現）、正接（タンジェントと読み式ではTanと表現）の3種
類があります。 更にそれらの逆関数としてアークサイン（Asinと表現)、
アークコサイン（Acosと表現）、アークタンジェント（Atanと表現）があり
ますが、それぞれの式は左の図のようになっています。
これらの三角関数においてある特定の角度に対しての値は覚えやすいの
で便利に使えます。 以下はそれらの一覧です。
| |
θ の値 |
| 三角関数 |
0度 |
30度 |
45度 |
60度 |
90度 |
| Sin(θ) |
0 |
0.5 |
1/√2 |
√3/2 |
1 |
| Cos(θ) |
1 |
√3/2 |
1/√2 |
0.5 |
0 |
| Tan(θ) |
0 |
1/√3 |
1 |
√3 |
∞ |
註） √2は、1.41421356（ヒトヨヒトヨニヒトミゴロ）、√3は、1.7320508
（ヒトナミニオゴレヤ）で覚えておくと良い。
実際の日曜大工作業においてはこれら全てを使うことはなく、タンジェント
とアークタンジェントだけで殆ど用が足ります。 従ってこれからの解説
は全てタンジェントまたはアークタンジェントだけで進めます。
さて上記の特異な角度以外の三角関数はどのように計算したらよいでしょ
うか？ 私が学生時代は計算尺を使って略算しました。 その後電子計算
機が登場して関数電卓が使えるようになり大変便利になりましたが、現在
ではそのためにお金を出さずとも関数計算が容易に出来ます。
そのひとつはパソコン上で動作する関数電卓のソフトウェアです。
私は右のようなM電卓と言うフリーソフトを5年ほど使っていますが、関数電
卓として必要な機能は全て持っており計算結果をそのままExcelのセルに
代入出来るので大変便利です。
試してみたい方はこちらから作者のホームページにアクセスしてダウンロードしてください。 使い方についてはここでは触れません。
もうひとつは表計算ソフトが持っている関数計算機能を使うことで、表計算
ソフトとして最もポピュラーなMS Excelでの使用例を後ほど紹介します。
 具体的な計算例
辛気臭いお話が長々と続くのは面白くありませんからタンジェン
ト、アークタンジェントの使い方を実例で示しましょう。
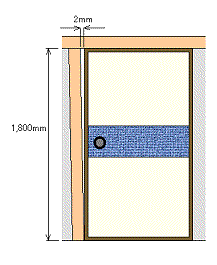
左の図は上のほうで触れた襖を閉めたときに上のほうに隙間が
出来る現象を表しており、柱の方が傾いている事にして、どの位
狂っているかを計算してみます。
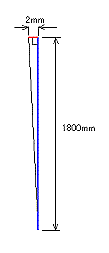
図の隙間だけを抜き出すと右の図のようになります。 これは
上に示したタンジェントを表す3角形を上下に伸ばして逆さにした
ようなものです。 従って左上の角は、Atan（1800/2)になりま
す。 この計算をM電卓でしてみると、89.94度と求まります。
つまり冒頭の方で述べたように0.06度狂っているわけです。
以上の例は2つの長さを求めてそこから角度を計算する場合です
が、その反対にある角度をなす線を引く場合の例を次に示します。
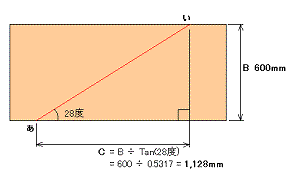左は幅が600mmある板に「あ」から「い」にかけて28度の傾斜をもつ
線を引く方法を引く方法を表しています。
前述のタンジェントの式の図でBの辺に相当する長さは600mmで、C
に相当する部分を算出せねばなりません。
ここで Tan(θ） = B/C を変形したC = B ÷ Tan(θ）という式より計
算すると1,128が求まります。
結論として「あ」と「い」の間の長さを1,128mmにすれば28度の傾斜
で線が描けることになります。
この方法で描く傾斜角度の精度はかなり高いのが特徴です。
例えば長さを1,130mmで描いた（2mmの誤差）とした場合の角度は27.97度で、0.03度の違いしかありません。 分度器や高価なプロトラクターを使ってもこれほど正確な角度の割付は絶対に出来ません。
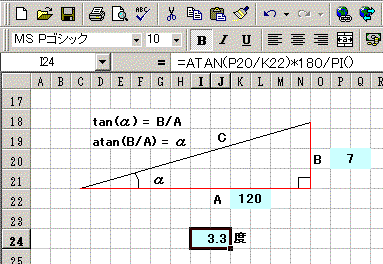 MS Excelで関数の計算をする方法
左は私が設計図を描く際に使うテンプレートに角度計算
を自動的にさせるための式を埋め込んだ例です。
空色で塗りつぶしたセルは正方形の小さなセルでは数
値を表示し切れないので、セルを連結しています。
現在のアクティブセルは、I24ですが、このセルには数
式バーで判るように、=ATAN(P20/K22)*180/PI()
という式が入っていますが、これはセル（K22）に入って
いる数値を底辺、セル（P22)に入っている数値を高さと
した時の角度（α）を算出する式です。 式の最後に入っ
ている *180/PI()は、Excel内で扱う標準の角度の単
位はラジアンですので、それを「度」に変換するためのも
のです。 PI()はπで3.14159・・・・を表します。
（ラジアンと度の関係は、2πラジアン = 360度である。）
ここでは実際に底辺の長さとして120を、高さとして7を
入れた場合で、その答えとして3.3度と出ていますが、底辺、高さ共に別な数値を入れれば瞬時にその時の角度が表示されます。
直角を割り付ける方法
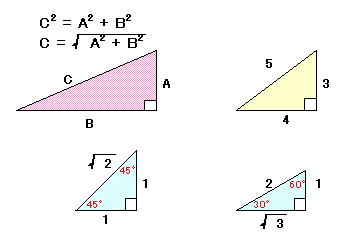大きな板を直角に切断しようとする場合先ず正確な線引きをし
ないとなりません。 こんな場合にはこれまで解説してきた三角
関数を使うまでもなく、ピタゴラスの定理を使って簡単に作業で
きます。 ピタゴラスの定理は左の図をご覧下さい。
直角三角形の直角を挟む辺それぞれの二乗の和は残りの
斜辺の二乗に等しい。
という式です。
実際に使う場合には平方根の計算が必要になりますが、特異
なケースが3種類あり、これらを覚えておけば平方根の計算無し
で直角の割付が可能です。
左の図の黄色で示した辺の比が3:4:5となる場合と、小中学校
で使った2種類の直角三角定規（空色）がそれらです。
3:4:5の比になる場合は整数だけで計算できますから最も利用
価値がありますので、それを使った直角な線引き方法を説明し
ます。
左の図がその方法です。 仮に、幅が910mmあるが端が直角ではない板に線を引いて
切断し直角にしないとならない！という状況だとします。
先ず910mmの板幅部分が前述の比率3:4:5の三角形の3に相当するとします。 線を引
きたいA点から板に沿って 910÷3x4=1,213mm離れた所に印をつけてCとします。
A-Cの部分は比率4に相当します。 次にC点の所にコンベックスの100mmの目盛りを
当てて、1,517mm離れたコンベックスの1,617mmの目盛りと板の縁が一致する点にB
を印します。 （1,517mmは、910÷3x5で求めた比率5に相当します。）
こうしてからA点とB点を結べばその線は板の長さ方向と直角になりますのでこれに沿っ
て切断すればOKです。（A、B、Cで出来る3角形は、Aの角が直角になり辺の比率が
3:4:5の直角三角形ということです。）
この方法で描いた直角の線の角度誤差もかなり小さいです。 例えば1,213mm離れたC点は正確に印したが、コンベックスでC点から1,517mm離れたB点の印しを1mm間違えて1,518mmで印したとします。
この時のA点の角度は90.13度と求められ＋0.13度の誤差となります。 C点、B点の印しを0.5mm以内の精度で付けられれば、±0.06度程度の誤差に収まり実用上支障の出る事は全くないでしょうし、無論プロトラクターや分度器でそのような正確な割付は全く不可能です。
Copyright (C) 2001-2019, Vic Ohashi All rights reserved.
|
HOME
